Trigonometric Functions Formulas - Single,Half,Double,Multiple Angles

Basic Trigonometric Functions
Definition of Trigonometric Functions For a Right Angle
Triangle ABC bas a right angle (9O°) at C and sides of length a, b, c. The trigonometric functions of angle A are defined as follows.
Extensions To Angles Which May be Greater Than 90°
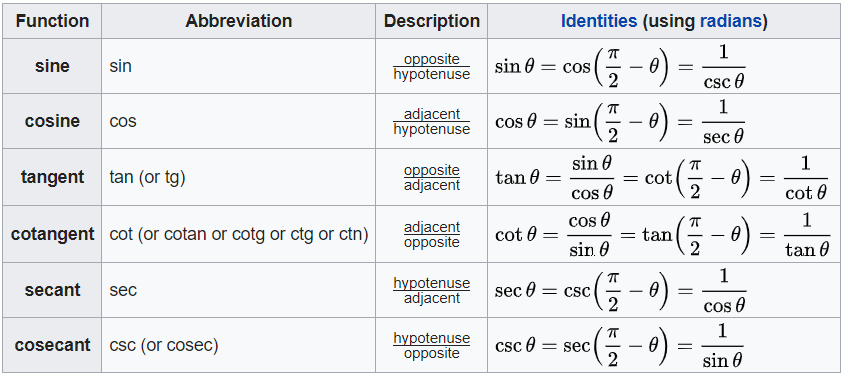
Consider an xy coordinate system . A point P in the xy plane has coordinates (x,y) where x is eonsidered as positive along OX and negative along OX´ while y is positive along OY and negative along OY´ .
The distance from origin 0 to point P is positive and denoted by r = √x2 + y2
The angle A described counterclockwise from OX is considered positive. If it is described dockhse from
OX it is considered negative. We cal1 X´ OX and Y´ OY the x and y axis respectively.
The various quadrants are denoted by 1, II, III and IV called the first, second, third and fourth quadrants respectively
For an angle A in any quadrant the trigonometric functions of A are defined as follows.
sin A = y/r
cos A = x/r
tan A = y/x
cet A = x/y
sec A = r/x
csc A = r/y
Signs And Variations Of Trigonometric Functions
tan A = Sin A / Cos A
Cot A = 1 / tan A = Cos A / Sin A
Sec A = 1 / Cos A
Csc A = 1 / Sin A
Sin2 A + Cos2 A = 1
Sec2 A - tan2 A = 1
Csc2 A - Cot2 A = 1
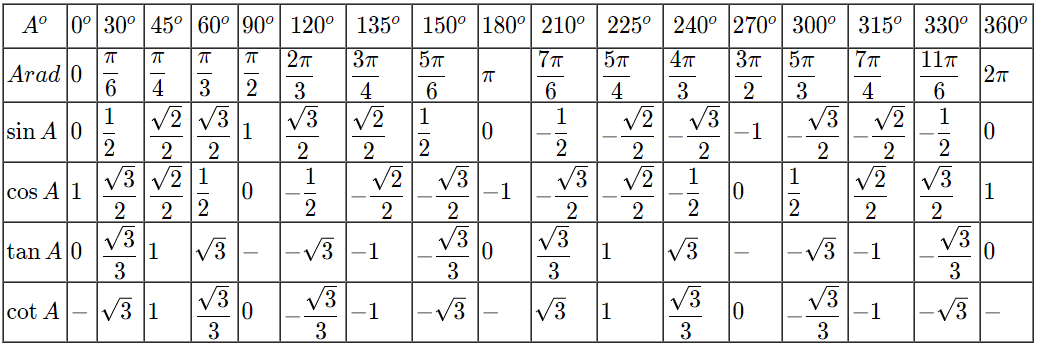
Exact Values For Trigonometric Functions Of Various Angles
Functions Of Negative Angles
Sin (-A) = - Sin A
Cos (-A) = Cos A
tan (-A) = - tan A
Csc (-A) = - Csc A
Sec (-A) = Sec A
Cot (-A) = - Cot A

Addition Formulas
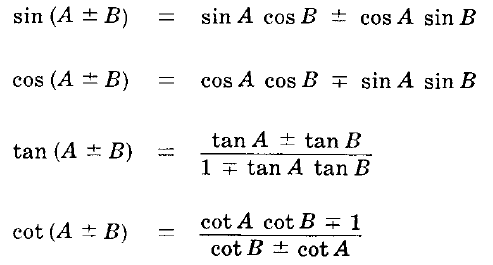
Functions Of Angles in All Quadrants in Terms Of Those in Quadrant I
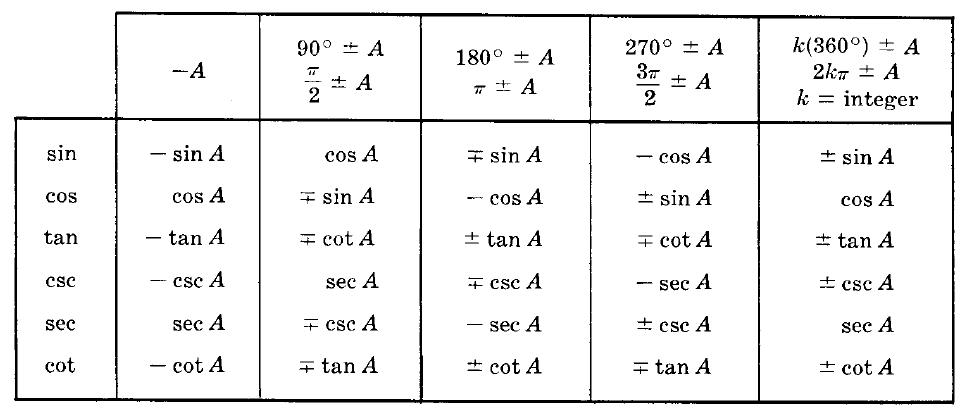
Relationships Amoung Functions Of Angles in Quadrant I
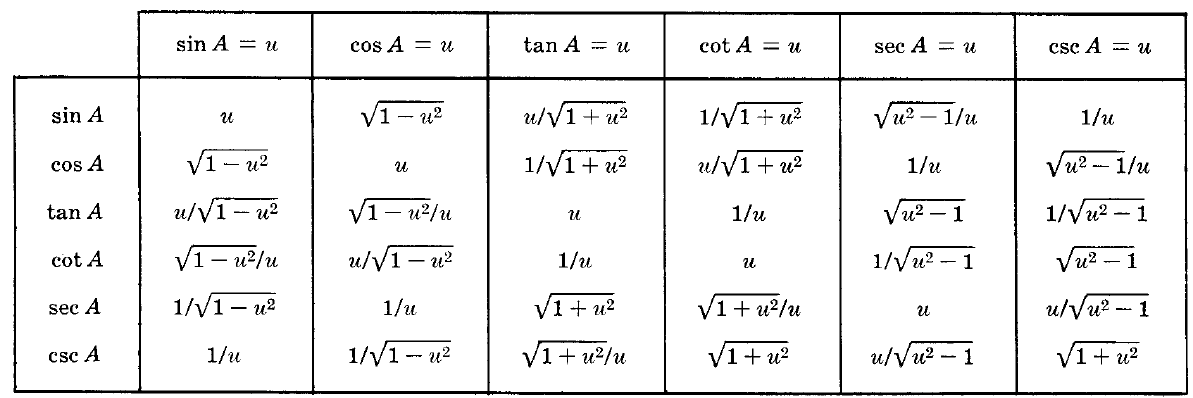
Double Angle Formulas
Sin 2A = 2 Sin A Cos A
Cos 2A = Cos2A - Sin2A = 1 - 2 Sin2A = 2 Cos2A - 1
tan 2A = 2 tan A / 1 - tan2A
Half Angle Formulas
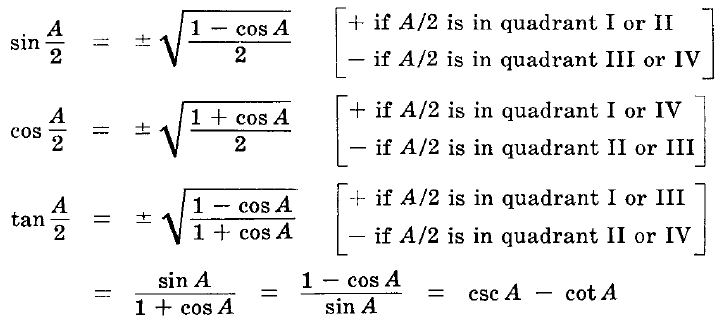
Multiple Angle Formulas
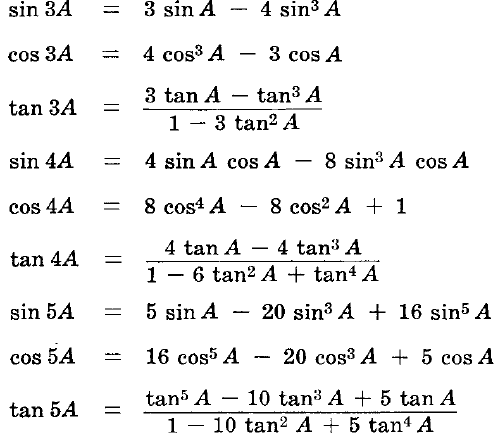
Powers of Trigonometric Functions

Sum, Difference and Product Of Trigonometric Functions
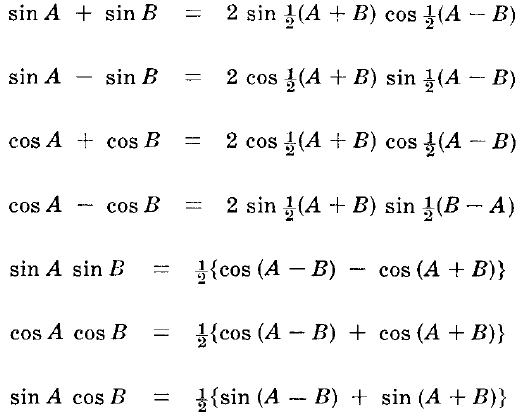
Powered by mymathtables.com
