Triangle Calculator

 This online angle calculator used to solves any triangles by entering the followings

2 sides and 1 angle (or)

2 angles and 1 side (or)

2 sides and 1 angle to find remaining values as used in trigonometry.

Enter 3 Positive Values and Click the "Calculate" button
(Including at least one side)

Side a

Side b

Side c

Left Angle (A)   °

Right Angle (B)  °

Top Angle (C)  °

Angle Units

°rad

      

 

Area of Triangle

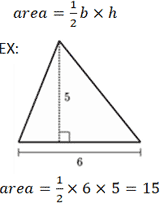
Calculating the area of a triangle involves its base, b, and height, h.

The base refers to any side of the triangle where the height is represented by the length of the line segment.

Area of Inner Radius

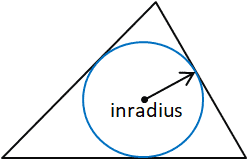
Inradius = Area / s

s = ( a + b + c ) / 2

where a, b, and c are the sides of the triangle

Four Triangle Facts

1) It is not possible for a triangle to have more than one vertex with internal angle greater than or equal to 90°, or it would no longer be a triangle.

2) The interior angles of a triangle always add up to 180° while the exterior angles of a triangle are equal to the sum of the 2 interior angles that are not adjacent to it.

3) Another way to calculate the exterior angle of a triangle is to subtract the angle of the vertex of interest from 180°.

4) The sum of the lengths of any 2 sides of a triangle is always larger than the length of the 3^rd side

Types of Triangle

Equilateral triangle

The Equilateral triangle shown on the left has 3 congruent sides and 3 congruent angles.Each angle is 60°

Isosceles triangle

The Isosceles triangle shown on the left has 2 equal sides and 2 equal angles

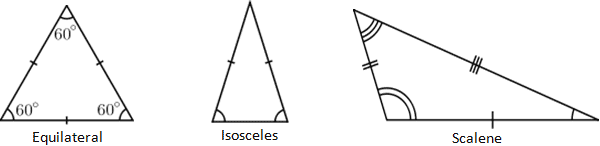
Scalene Triangle

The Scalene Triangle has no congruent sides. In other words, each side must have a different length.

Acute Triangle

The Acute Triangle has 3 acute angles (an acute angle measures less than 90°)

Obtuse Triangle

The Obtuse Triangle has an obtuse angle (an obtuse angle has more than 90°)

Since the total degrees in any triangle is 180°, an obtuse triangle can only have one angle that measures more than 90°.