Basic Fourier Series Formula List in PDF

 Engineering Mathematics: Fourier Series Formula pdf
Engineering Mathematics: Fourier Series Formula pdf
An online fourier series formulas printable
Fourier Series
 Print This Page Print This Page  Download This Page Download This Page |
|---|
1. Fourier Series - Introduction Jean Baptiste Joseph Fourier (1768-1830) was a French mathematician, physicist and engineer, and the founder of Fourier analysis.Fourier series are used in the analysis of periodic functions. The Fourier transform and Fourier's law are also named in his honour. |
2. Fourier Series of Even and Odd Functions
A function f(x) is said to be even if f(-x) = f(x).
The function f(x) is said to be odd if f(-x) = -f(x)
Graphically, even functions have symmetry about the y-axis,whereas odd functions have symmetry around the origin.
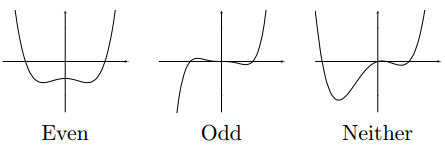
Examples:
Sums of odd powers of x are odd: 5x3- 3x
Sums of even powers of x are even: -x6 + 4x4+ x2-3
sin x is odd, and cos x is even
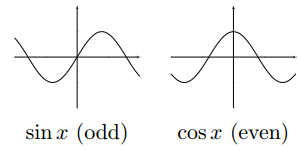
The product of two odd functions is even: x sin x is even
The product of two even functions is even: x2cos x is even
The product of an even function and an odd function is odd: sin x cos x is odd
3. Integrating even functions over symmetric domains.
Let p > 0 be any fixed number. If f(x) is an odd function, then

Intuition: The area beneath the curve on [-p, 0] is the same as the area under the curve on [0, p], but opposite in sign. So, they cancel each other out!

Let p > 0 be any fixed number. If f(x) is an even function, then

Intuition: The area beneath the curve on [-p, 0] is the same as the area under the curve on [0, p], but this time with the same sign. So, you can just find the area under the curve on [0, p] and double it!

4. Periodic functions
Definition:
A function f(x) is said to be periodic if there exists a number
T > 0 such that f(x + T) = f(x) for every x. The smallest such
T is called the period of f(x).
Intuition: periodic functions have repetitive behavior.A periodic function can be defined on a finite interval,
then copied and pasted so that it repeats itself.

5. The fourier series of the function f(x)
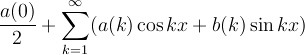
a(k) =f(x) cos kx dx
b(k) =f(x) sin kx dx
6. Remainder of fourier series
Sn(x) = sum of first n+1 terms at x.
remainder(n) = f(x) - Sn(x) = 
 f(x+t) Dn(t) dt
f(x+t) Dn(t) dt
Sn(x) = 
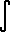
 f(x+t) Dn(t) dt
f(x+t) Dn(t) dt
Dn(x) = Dirichlet kernel =
Comments
The Dirichlet kernel is also called the Dirichlet summation kernel. There is also a different normalization in use: the kernels Dn and  are often multiplied by 2. They are then represented also by the series
are often multiplied by 2. They are then represented also by the series
 |
7. Riemann's Theorem
.If f(x) is continuous except for a finite # of finite jumps in every finite interval then:
lim(k-> )
)
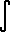
 f(t) cos kt dt = lim(k->
f(t) cos kt dt = lim(k->
 )
)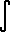
 f(t) sin kt dt = 0
f(t) sin kt dt = 0
The fourier series of the function f(x) in an arbitrary interval.
A(0) / 2 +
 (k=1..
(k=1.. )
[ A(k) cos (k(Π)x / m) + B(k) (sin k(Π)x / m) ]
)
[ A(k) cos (k(Π)x / m) + B(k) (sin k(Π)x / m) ]
a(k) = 1/m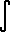
f(x) cos (k(Π)x / m) dx
b(k) = 1/m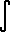
f(x) sin (k(Π)x / m) dx
8. Parseval's Theorem
.Parseval's theorem usually refers to the result that the Fourier transform is unitary, that the sum (or integral) of the square of a function is equal to the sum (or integral) of the square of its transform.
If f(x) is continuous; f(-PI) = f(PI) then

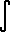
 f2(x) dx = a(0)2 / 2 +
f2(x) dx = a(0)2 / 2 +
 (k=1..
(k=1.. ) (a(k)2 + b(k)2)
) (a(k)2 + b(k)2)
Fourier Integral of the function f(x)
f(x) = 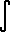
 ( a(y) cos yx + b(y) sin yx ) dy
( a(y) cos yx + b(y) sin yx ) dy
a(y) =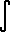
f(t) cos ty dt
b(y) =f(x) =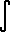
f(t) sin ty dt

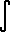
 dy
dy 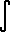
 f(t) cos (y(x-t)) dt
f(t) cos (y(x-t)) dt
9. Special Cases of Fourier Integral
if f(x) = f(-x) then
f(x) =if f(-x) = -f(x) then
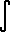
cos xy dy
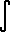
f(t) cos yt dt
f(x) =
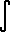
sin xy dy
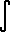
sin yt dt
10. The Fourier Transforms
Fourier Cosine Transform
g(x) = 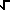 (
( )
)
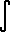
 f(t) cos xt dt
f(t) cos xt dt
Fourier Sine Transform
g(x) = 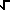 (
( )
)
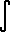
 f(t) sin xt dt
f(t) sin xt dt
11. Identities of the Transforms
If f(-x) = f(x) then
Fourier Cosine Transform ( Fourier Cosine Transform (f(x)) ) = f(x)
If f(-x) = -f(x) then
Fourier Sine Transform (Fourier Sine Transform (f(x)) ) = f(x)Powered by mymathtables.com

