Basic-Algebra-Polynomial-Exponential-Logarithms Identities

Practice Prime Numbers | Even Numbers | Odd Numbers | Other Number Charts
Basic Algebra Identities |
| Closure Property of Addition |
| Sum (or difference) of 2 reals equals a real number |
| Additive Identity |
| a + 0 = a |
| Additive Inverse |
| a + (-a) = 0 |
| Associative of Addition |
| (a + b) + c = a + (b + c) |
| Commutative of Addition |
| a + b = b + a |
| Definition of Subtractio |
| a - b = a + (-b) |
| Closure Property of Multiplication |
Product (or quotient if denominator 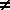 0) of 2 reals equals a real number 0) of 2 reals equals a real number |
| Multiplicative Identity |
| a * 1 = a |
| Multiplicative Inverse |
a * (1/a) = 1 (a 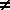 0) 0) |
| (Multiplication times 0) |
| a * 0 = 0 |
| Associative of Multiplication |
| (a * b) * c = a * (b * c) |
| Commutative of Multiplication |
| a * b = b * a |
| Distributive Law |
| a(b + c) = ab + ac |
| Definition of Division |
| a / b = a(1/b) |

Basic Polynomial Identities |
| Binomial Theorem |
| (a+b)2 = a2 + 2ab + b2 |
| Multiply Binomials |
| (a+b)(c+d) = ac + ad + bc + bd |
| Difference of Squares |
| a2 - b2 = (a+b)(a-b) |
| Sum and Difference of Cubes |
a3 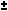 b3 = (a b3 = (a 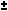 b)(a2 b)(a2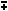 ab + b2) ab + b2) |
| x2 + (a+b)x + ab = (x + a)(x + b) |
| Basic Quadratic Identities |
If ax2 + bx + c = 0 then x = ( -b 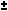 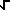 (b2 - 4ac) ) / 2a (b2 - 4ac) ) / 2a |
Basic Exponential Identities (Powers) |
| x a x b = x (a + b) |
| x a y a = (xy) a |
| (x a) b = x (ab) |
x (a/b) = bth root of (x a) = ( bth 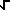 (x) ) a (x) ) a |
| x (-a) = 1 / x a |
| x (a - b) = x a / x b |
Logarithms Basic |
| y = logb(x) if and only if x=b y |
| logb(1) = 0 |
| logb(b) = 1 |
| logb(x*y) = logb(x) + logb(y) |
| logb(x/y) = logb(x) - logb(y) |
| logb(x n) = n logb(x) |
| logb(x) = logb(c) * logc(x) = logc(x) / logc(b) |
